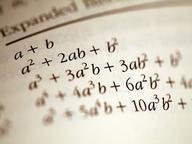Quiz Answer Key and Fun Facts
1. When given a relatively basic quadratic question such as x^2 + 9x + 20, which of these options is a suitable way to solve it?
2. What would be the two constituents of the following quadratic question: x^2 + x - 6?
3. Basic arithmetic will be important in your attempt to solve the next question. What are the two constituents of x^2 - 9x + 18?
4. Quadratics are not always basic and often the x^2 term will have a co-efficient greater than 1. What are the two components of the following: 3x^2 + 9x + 6? (There are other possibilities, however, only one of the following answers is correct)
5. An equation is a phrase which contains an equals (=) sign and is therefore able to be solved to give roots (answers). In quadratics there are two answers (which may, however be imaginary, complex or identical). Solve the following equation: x^2 - 4x + 4 = 0.
6. Solve the following quadratic equation: x^2 + 2x - 8 = 0.
7. In those dreaded maths examinations, students are often given the components and are asked to find the original quadratic expression. Find the expression from the following constituents: (x+8) and (x-3).
8. Find the expression from the given components: (x-6) and (x-4).
9. The topic of quadratics does indeed have an equation, and boy is it an equation! X = -b ± (?) / 2a. Within this equation you will see a missing portion indicated by a question mark in brackets/parentheses. (?) = the square root of what?
10. Quadratic equations can also be shown graphically. If the quadratic expression was positive: y = 3x^2 + x - 2, what shape would the graphical curve be?
Source: Author
jonnowales
This quiz was reviewed by FunTrivia editor
crisw before going online.
Any errors found in FunTrivia content are routinely corrected through our feedback system.