3. What property is not found in every ring?
From Quiz An Adventure in Abstract Algebra
Answer:
Commutative multiplication
Rings include all of the common properties for addition (closure, commutative, associative, identity, and inverses) along with the distributive law, closure under multiplication, and associative multiplication. Closure means that you cannot move out of the set when performing the operation. For example, integers are not closed under division because 3 divided by 19 is NOT an integer. Special rings can include combinations of commutative multiplicative (commutative rings), identity (rings with identity), and inverse (division rings). If a ring has ALL of these properties it is called a field.
These rules form a natural progression when learning arithmetic. We learn about adding and multiplying natural numbers but natural numbers are very limited (you can't have a problem like 3-8). We then proceed to integers which is the ring formed by the natural numbers, zero, and their inverses. This new system lets us do more but we still have a problem with division. What is -17 divided by 2 using long division? Is it -9r+1 or -8r-1? We need to have multiplicative inverses and so we take the integers and create the field of rational numbers commonly known as fractions. Now you know why math after 5th grade is so dependent on fractions.
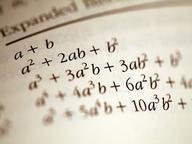



 Quick Question
Quick Question = Top 5% Rated Quiz,
= Top 5% Rated Quiz,
 Top 10% Rated Quiz,
Top 10% Rated Quiz,