27. Add the binary numbers 101 and 111 together. Give your answer in binary form.
From Quiz Operations in That Scary Binary System!
Answer:
1100
I find the easiest way to add binary numbers is to convert them into base ten and add them together then. You can then change the number back into the binary system. Keep in mind that the last slot in a binary number is 2^0, not 2^1, which means when there are, say, 5 digits in a binary number, the first number is in the 2^4 slot, not the 2^5 slot. The binary system is based on powers of two, so 101 is equal to (2^2 * 1) + (2^1 * 0) + (2^0 * 1). Simplify that into 4 + 0 + 1, or 5. Do the same with 111, your other binary number. (2^2 * 1) + (2^1 * 1) + (2^0 * 1), which can be simplified to 4 + 2 + 1, which is equal to 7. Take your two numbers that are in base ten, 5 and 7, and add them together to get 12. Change that into a binary number by determining which powers of two add up to twelve. If you try 2^4 (which is 16) first, you will see that 16 is larger than 12, and a 1 cannot be in the 2^4 spot. Try 2^3, which is 8. You will see that it is smaller than 12 and therefore can have a 1 put in its place. Progress on to 2^2, which is 4. You have 4 left over with your 12, so stick a 1 in that place. Place zeros in the 2^1 and 2^0 place value slots, because you have your number. Your binary number for 12 is 1100.


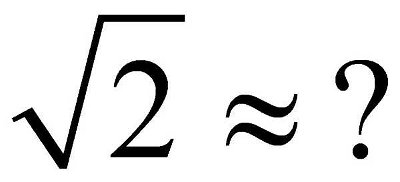

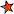

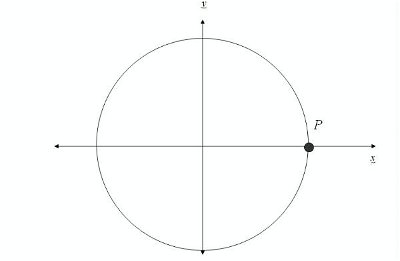

 Quick Question
Quick Question = Top 5% Rated Quiz,
= Top 5% Rated Quiz,
 Top 10% Rated Quiz,
Top 10% Rated Quiz,